Thermodynamics is a very beautiful subject which helps us to understand working and governing behaviour of the Universe, to begin with and make things simpler, we start with operating under ideal gas equations and go on to those real life situations which not only involve thermal equations but mechanics and general physics as well.
As it involves real case scenarios many dissipation forces come into existence which makes it even more complex to deal with those problems. For example, most of the theories which we study in thermodynamics and most common form of work we compute is displacement work.
The differential formula for work done by a gas is given by:
dW = -PdV
Where dW is the infinitesimal amount of work done by the gas, P is the pressure of the gas, and dV is the infinitesimal change in volume of the gas.
This very famous equation for work computation is something which you would have seen many times while studying first law and work energy equations. But how much solving this can be justified to solve real life problems based on thermodynamics?
Due to irreversible nature of the Universe, most of the thermodynamic process which we see today are actually not quasi-static process.
So what is a quasi static process.
Take an example of a thermodynamic process where a gas, take air for simplicity is taken from a state where it’s pressure is P1,V1 to a state where it’s pressure goes to P2,V2. Now based on the nature of process (adiabatic/ isothermal/ isobaric/ isochoric) the entire setup could be sliced down into very small small reversible processes which adds ease to compute those variables, net work done and other parameters as well. This type of step by step or we can say every step equilibrium process is referred to as quasi static process.
In case of most of the real world thermodynamic processes, work is generally computed by the first law equation that is:
Q=W+U
Where Q is net heat supplied/ liberated and U is the internal energy of the system. Also note that Q doesn’t mean absolute Q but it’s the change of overall heat energy from the beginning to the end.
Heat energy has fascinated researchers and physicians from long back and given them hard time to actually understand this strange physical quantity.
Initially the caloric theory of heat was proposed which treated heat as an invisible fluid which perhaps suited to the best explanation of what is heat whereas years later sir James Prescott Joule came up with his more sensible theory which described heat as a work equivalent and equated the two quantities showing their linear dependencies to each other. The equation is given as:
Q=JW
Where J is the constant of proportionality, later this theory became highly popular and helped to relate all its physical observations and phenomenon with much ease.
Coming back to the original discussion, since there are considerable amount of differences in real world thermodynamics and the one which we study in books, an efficient way to approach the problem is via Computers, we can create powerful programs to simulate the real world scenarios and look for optimizations as there would be accurate results, more iterations and beautiful visualizations. Though I am not criticizing anything about existing curriculum or whatever we study now in thermodynamics which is also very very important to help us understand the concepts better and get a better view of what actually happens before directly jumping into the broad and complex scenarios.
So here, I will be discussing how can we possibly compute work done by a real gas in a isothermal thermodynamic process. Further the method will be implemented using Matlab which is one of my favourite numerical computation software and so we will generalize a case, take the input compute the work and visualize accordingly. Before actually diving into the problem, I would recommend everyone who is new to thermodynamics to give a read about displacement work and various thermodynamic processes and how their work equations are computed. This will be really helpful to proceed further with getting a in depth understanding of what I will be doing.
So let’s begin this:
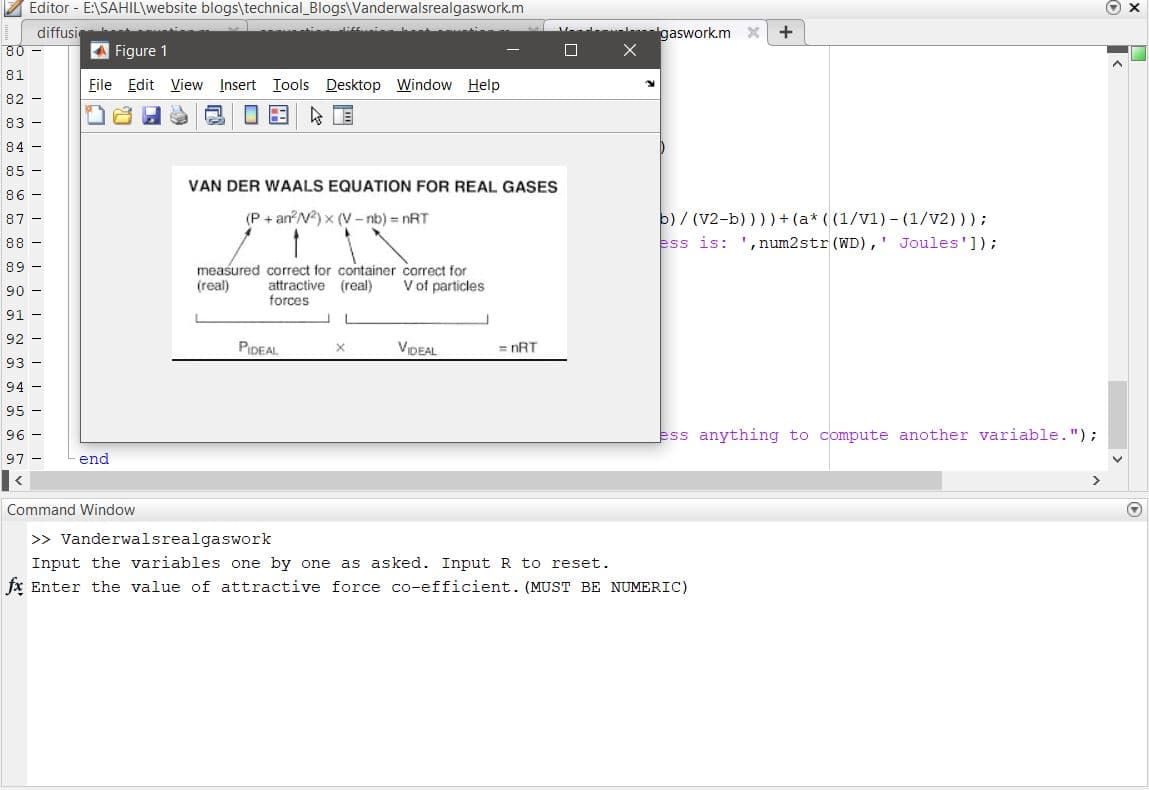
We all know real gas equation is as follows:

Looks a little too complicated? Well don’t worry, just flow with the basics and break down these monstrous terms slowly and slowly.
Now for any real gas, at two different points:
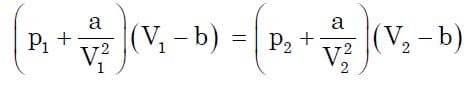
Let’s assume the above expression to be equal to a constant K which is nothing but RT (for unit mass) (which is constant)
Now expression for displacement work is given by:
Integral (Pdv)
Sending v-b to RHS to obtain p in terms of v we get:
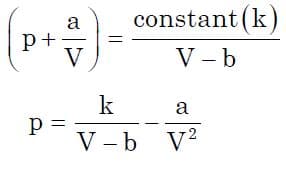
Finally, this is the main goal of almost any thermodynamic process to compute it’s work expression. Once we obtain p in terms of V, we just need to substitute it into displacement work equation to obtain the required term. Now substituting the following expression and integrating for the limits from v1 to v2, we get:
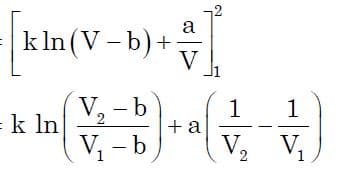
On further simplification and substituting value of k in terms of P1 we get:
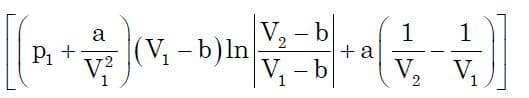
which is the expression we were seeking for. Now based on this equation, we can obtain the work done by real gas in isothermal process.
Since we have obtained our expressions theoretically let’s implement it in Matlab. User can give the information in terms of anything for example P1,V1 and V2 or P1,V2 and P2, accordingly we have to take the input, take care of boundary conditions which are:
- V1 must not be equal to zero.
- V1 must not be equal to b.
- V2 must not be equal to zero.
First let’s begin with taking the inputs. We must ensure that all the inputs should be in numeric form and logarithmic value should not be negative (in case we may get imaginary terms). Also since volumetric equation may go a bit complex as we have square term in denominator and linear term in numerator. To carefully compute, we can assume (a/V1)^2 as negligible as a is very small and it adds very little to actual value, this helps in computing V1 easily and hence reducing complexity. Here is the code:
%Vanderval’s real gas work done in an isothermal process
VE=imread(‘1.JPG’);
%To display vanderWal’s equation
imshow(VE);
disp(‘Input the variables one by one as asked. Input R to reset.’); %Reset used to re enter the variables
val=’K’;
while (val~=’Q’)
a=input(‘Enter the value of attractive force co-efficient.(MUST BE NUMERIC)’);
if(~isnumeric(a))
disp(‘Value of a must be a numeric value. Resetting all values! Input again.’);
else
b=input(‘Enter the value of Volume Correction factor. (MUST BE NUMERIC)’);
if(~isnumeric(b))
disp(‘Value of b must be a numeric value. Resetting all values! Input again.’);
else
disp(‘Awesome! a and b datas have been recorded. To proceed with work computation, Choose the known inputs.’);
choice=input(‘\n\nFor unknown: \nP1 enter —> 1.\nP2 enter –> 2.\nV1 enter 3.\nV4 enter –> 4.’);
if(~isnumeric(choice))
disp(‘Choice must be between 1 and 4.’);
else
if(choice<1||choice>4)
disp(‘Choice must be between 1 and 4.’);
else
if(choice==1)
P2=input(‘Enter value of final pressure.(in N/m2)’);
V1=input(‘Enter value of initial volume. (in m3)’);
V2=input(‘Enter value of final volume. (in m3)’);
if(~isnumeric(P2)||~isnumeric(V1)||~isnumeric(V2))
disp(‘Invalid input’);
else
%Computing p1:
temp=(V2-b)/(V1-b);
P1=temp*(P2+(a/V2)^2);
if(b==V2||b>V2||b>V1||V1==0||V2==0)
disp(‘Invalid Input’);
else
WD=((P1+(a/V1)^2)*(V1-b)*(log((V1-b)/(V2-b))))+(a*((1/V1)-(1/V2)));
disp([‘Work done in the given process is: ‘,num2str(WD),’ Joules’]);
end
end
elseif(choice==2)
P2=input(‘Enter value of final pressure.(in N/m2)’);
P1=input(‘Enter value of initial pressure. (in N/m2)’);
V2=input(‘Enter value of final volume. (in m3)’);
if(~isnumeric(P2)||~isnumeric(P1)||~isnumeric(V2))
disp(‘Invalid input’);
else
%Computing p1:
temp=(P2+(a/V2)^2)/P1;
V1=(temp*(V2-b))+b;
if(b==V2||b>V2||b>V1||V1==0||V2==0)
disp(‘Invalid Input’);
else
WD=((P1+(a/V1)^2)*(V1-b)*(log((V1-b)/(V2-b))))+(a*((1/V1)-(1/V2)));
disp([‘Work done in the given process is: ‘,num2str(WD),’ Joules’]);
end
end
elseif(choice==3)
P1=input(‘Enter value of initial pressure.(in N/m2)’);
V1=input(‘Enter value of final Volume. (in m3)’);
V2=input(‘Enter value of final volume. (in m3)’);
if(~isnumeric(P1)||~isnumeric(V1)||~isnumeric(V2))
disp(‘Invalid input’);
else
if(b==V2||b>V2||b>V1||V1==0||V2==0)
disp(‘Invalid Input’);
else
WD=((P1+(a/V1)^2)*(V1-b)*(log((V1-b)/(V2-b))))+(a*((1/V1)-(1/V2)));
disp([‘Work done in the given process is: ‘,num2str(WD),’ Joules’]);
end
end
else
P1=input(‘Enter value of initial pressure.(in N/m2)’);
P2=input(‘Enter value of final pressure. (in N/m2)’);
V1=input(‘Enter value of initial volume. (in m3)’);
if(~isnumeric(P2)||~isnumeric(P1)||~isnumeric(V1))
disp(‘Invalid input’);
else
%Computing p1:
temp=(P1+(a/V1)^2)/P2;
V2=(temp*(V1-b))+b;
if(b==V2||b>V2||b>V1||V1==0||V2==0)
disp(‘Invalid Input’);
else
WD=((P1+(a/V1)^2)*(V1-b)*(log((V1-b)/(V2-b))))+(a*((1/V1)-(1/V2)));
disp([‘Work done in the given process is: ‘,num2str(WD),’ Joules’]);
end
end
end
end
end
end
end
val=input(“Process finished, press ‘Q’ to quit else press anything to compute another variable.”);
end
I know it goes too long, but its just simple logic to ensure inputs and outputs are accurately computed. Though, I have added few comments to make it more readable but still there are many places where it may go confusing, you can ask your doubts in the comment and I will get to you asap.
Here are some of the outputs I got:
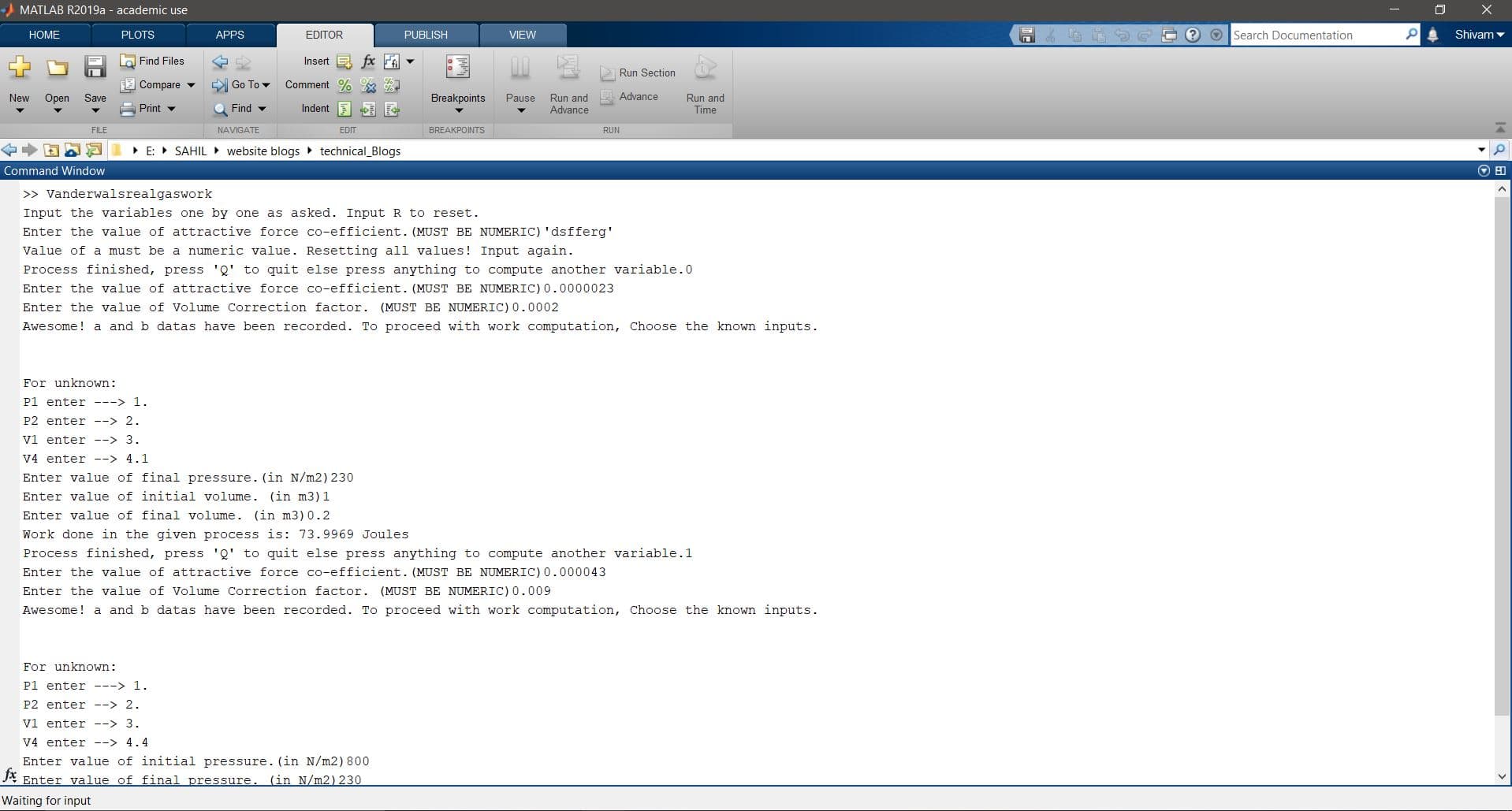
Hope this helped you in some way. See you in the next section soon. :X)
References: Engineering Thermodynamics
